Kosmografie (bouwfysica)
Contents
Beweging van de aarde om de zon
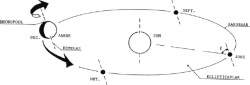
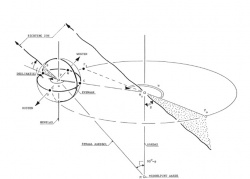
Bekeken wordt allereerst de baan, die door het middelpunt van de aarde wordt beschreven om de zon. Deze baan, gelegen in het eclipticavlak, is elliptisch van vorm en wordt aardbaan genoemd. Zie figuur 1.
De zon bevindt zich in een der brandpunten van de ellips en verdeelt de lange as van die ellips in stukken met een lengte van 147.106 km en 152.106 km. De aardbaan is dus nagenoeg cirkelvormig. De aarde doorloopt in een jaar eenmaal de aardbaan. De denkbeeldige as door het centrum van de ellips, loodrecht op het eclipticavlak, wordt ecliptica-as genoemd.
Vervolgens wordt gekeken naar de rotatie van de aardbol om de hemelas (verlengde van de aardas). De rotatiesnelheid is constant en het aantal omwenteling per jaar is nagenoeg gelijk aan driehonderdzesenzestig. e richting van hemelas, beschreven in een in het eclipticavlak gelegen assenstelsel assenstelsel, mag als onveranderlijk worden beschouwd. De hoek α tussen hemelas en ecliptica-as bedraagt 23,46°. Voor de kenmerkende data in een jaar, 22 december (kortste dag), 21 maart (begin van de lente), 21 juni (langste dag) en 23 september (begin van de herfst), geldt voor de in figuur 1 getekende hoek β tussen hemelas en verbindingslijn aarde-zon respectievelijk: β = 90° + α, β = 90°, β = 90° - α en β = 90°.
Plaatsbepaling op het aardoppervlak
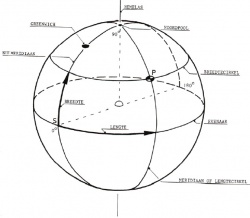
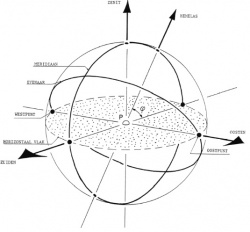
Voor de plaatsbepaling van een punt P op het aardoppervlak zijn de volgende in figuur 2 aangegeven, begrippen van belang:
- evenaar: doorsnijding van de aardbol met een plat vlak door het middelpunt van de aarde, loodrecht op de aardas.
- breedtecirkel : doorsnijding van de aardbol met een plat vlak door punt P, loodrecht op de aardas.
- meridiaan of lengtecirkel: de halve cirkelboog door de noordpool, punt P en de zuidpool.
- nulmeridiaan: de bij de plaats Greenwich behorende meridiaan.
- lengte: het stuk cirkelboog langs de evenaar, gemeten vanuit punt S tot aan het snijpunt van de Meridiaan door P met de evenaar. Punt S is het snijpunt van de nulmeridiaan met de evenaar. De lengte wordt uitgedrukt in de daarmee corresponderende middelpuntshoek. Zowel bij meting in oostelijke- als in westelijke richting kan deze hoek maximaal 180° bedragen
- breedte: als vorig punt, nu echter gemeten langs de (nul) Meridiaan. Zowel bij meting in noordelijke- als in zuidelijke richting kan de middelpuntshoek 90° bedragen.
Hemelstreken
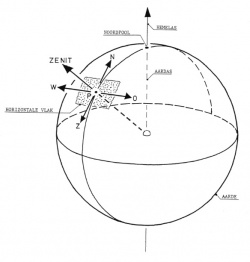
Het horizontale vlak in punt P van het aardoppervlak is het raakvlak aan de aardbol in dat punt. Zie figuur 3. De lijn vanuit het middelpunt van de aarde door punt P staat loodrecht op het horizontale vlak en wordt "verticaal" genoemd. Het verlengde van deze lijn heet het zenit.
De snijlijn, gevormd door het horizontale vlak en het platte vlak door de vertikaal en de hemelas, is de noord-zijdlijn. Loodrecht op de noord-zuidlijn ligt in het horizontale vlak de oost-westlijn.
De richting van een ster
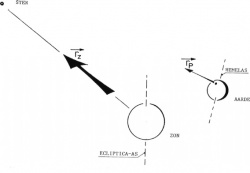
De richting van een ster, gezien vanuit de zon, wordt vastgelegd doormiddel van de richtingsvector 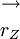 . De richting, waarin dezelfde ster wordt gezien vanuit een punt P van het aardoppervlak, wordt vastgelegd doormiddel van
. De richting, waarin dezelfde ster wordt gezien vanuit een punt P van het aardoppervlak, wordt vastgelegd doormiddel van 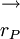 . Zie figuur 4.
. Zie figuur 4.
Omdat de afstand tussen zon en ster oneindig veel groter is dan de lengte van de, door de zon in de ruimte gedurende een etmaal afgelegde weg, verandert 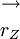 per etmaal niet. Om dezelfde reden geldt dit ook voor
per etmaal niet. Om dezelfde reden geldt dit ook voor 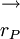 .
.
De afstand tussen een punt van het aardoppervlak en de zon is verwaarloosbaar ten opzichte van de afstand tussen zon en ster, zodat kan worden gesteld:
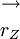 //
// 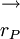 .
.
Voor de positie van de aarde ten opzichte van de zon geldt eveneens, dat deze per temaal als onveranderlijk is te beschouwen. Verder is de straal van de aardbol verwaarloosbaar ten opzichte van de afstand tussen zon en aarde. Hieruit volgt, dat de verbindingslijn tussen een punt van het aardoppervlak en het middelpunt van de zon evenwijdig loopt met de verbindingslijn tussen het middelpunt van de aarde en het middelpunt van de zon.
Op grond van hetgeen in deze paragraaf is vermeld, kan de volgende conclusie worden getrokken:
De hoek tussen de hemelas en de lijn, vanuit een pun van het aardoppervlak in de richting van de zon of een ander hemellichaam, is per etmaal als onveranderlijk te beschouwen.
Plaatsbepaling van een ster aan de hemel
Onafhankelijk van de plaats op aarde
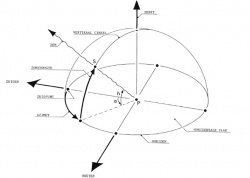
In punt P van het aardoppervlak wordt een lijn opgericht evenwijdig aan de hemelas. Deze lijn, eveneens hemelas genoemd, ligt in het platte vlak dat door de verticaal (zenit) en de noord-zuidlijn wordt opgespannen. Zie figuur 5. Om punt P wordt een bol geslagen. De doorsnijding van deze bol met een plat vlak, door punt P en loodrecht op de hemelas, wordt evenaar genoemd. De doorsnijding van de bol met een plat vlak, evenwijdig aan de evenaar, heet breedtecirkel. Onder de meridiaan wordt verstaan de doorsnijding van de bol met een plat vlak, opgespannen door zenit en hemelas. De ten oosten en ten westen van punt P gelegen snijpunten van de evenaar met het horizontale vlak worden respectievelijk oostpunt en westpunt genoemd. De lijn door deze punten is de oost-westlijn. De kleinste hoek tussen hemelas en de noord-zuidlijn is gelijk aan de breedtegraad van punt P.Deze hoek, aangegeven met de letter φ, is voor Nederland gemiddeld 52°.
Op soortgelijke wijze als in de paragraaf over plaatsbepaling op het aardoppervlak. is beschreven, kan nu met behulp van booglengten langs evenaar en meridiaan het snijpunt van de bol met de verbindingslijn tussen het punt P en een hemellichaam worden vastgelegd. Een en ander is te zien in Figuur 6. Hierin zijn de hemelas door punt P en de evenaar rond dit punt nogmaals getekend.
De plaats van punt B kan nu worden vastgelegd door het stuk cirkelboog COA langs de evenaar, gemeten vanuit punt C, en het stuk cirkelboog langs de meridiaan, overeenkomend met het stuk cirkelboog AB. De halve cirkelboog door de noordpool, punt B en de zuidpool heet declinatiecirkel. De middelpuntshoeken, behoren bij de booglengten COA en AB, worden respectievelijk uurhoek u en declinatie d genoemd. Zie figuur 6. Hoek u varieert in de getekende richting van 0° tot 360°. De deklinatie varieert tussen de -90° en +90°. Een deklinatie in noordelijke richting is positief, in zuidelijke richting negatief.
Tengevolge van de rotatie van de aardbol om de aardas beschrijft punt P een cirkelvormige baan, die in 24 uur eenmaal wordt doorlopen. Het vlak, waarin deze baan in gelegen, snijdt het vlak dat wordt opgespannen dor de aardas en de verbindingslijn tussen de zon en met punt M0 volgens de lijn P0P1. Eenvoudig is te bewijzen, dat het platte vlak door de punten P, A en B altijd evenwijdig is met het platte vlak door de punten M, P0 en F1. Omdat de punten P0, M0, P en A in één plat vlak liggen, geldt dus altijd dat de lijnen PA en P0M0 evenwijdig lopen. De oost-westlijn staat altijd loodrecht op de lijn PM0. In verband hiermee heeft een draaiing van de lijn PM0 ten opzichte van de lijn P0M0 over een hoek u voor de warnemer in punt P tot gevolg, dat hij lijn PA ziet draaien ten opzichte van lijn PM0 over dezelfde hoek u, echter in tegengestelde richting. Wanneer dit wordt gecombineerd met ht feit, dat hoek β per etmaal onveranderlijk is (zie conclusie in paragraaf De richting van een ster) kan de volgende conclusie worden getrokken:
Hemellichamen, die niet in het verlengde van de hemelas liggen beschrijven schijnbare cirkels in platte vlakken loodrecht op de hemelas.
De bij een hemellichaam behorende deklinatie is dus per etmaal als constant te beschouwen; de daarbij behorende uurhoek is een functie van de tijd. Het punt P0 is het verst van de zon verwijderde punt van de door punt P beschreven cirkelbaan. Het moment, waarop P zich in P0 bevindt, wordt middernacht genoemd en komt dus overeen met 0.00 uur. Tengevolge van de constante rotatiesnelheid van de aardbol bevindt P zich om 12.00 uur n punt P1. Na t uren is de lijn PM0 gedraaid over een hoek u = t x 15°. De halve cirkels door de noordpool, punt A en de zuidpool op de tijdstippen t = 0, 1, 2, … 24 uur worden uurcirkels genoemd. Zo liggen bijv. oostpunt en westpunt respectievelijk op de 6-uurcirkel en de 18-uurcirkel.
In figuur 6. is aangegeven, hoe de plaats van de zon aan de hemel kan worden vastgelegd. De plaatsbepaling van een willekeurig hemellichaam verloopt geheel analoog. Wanneer de lijn PA bij een hemellichaam, een hoek u = 180° maakt met de lijn PM0 dan is de hoek tussen de lijn vanuit P, in de richting van dat hemellichaam, en het horizontale vlak maximaal. Deze hoogte stand wordt culminatiepunt genoemd.
Uit het zojuist behandelde kan de volgende conclusie worden getrokken:
Wanneer de plaats van een hemellichaam wordt vastgelegd in het zojuist besproken assenstelsel, geldt dat de daarbij horende uurhoek en deklimatie op een gegeven tijdstip in ieder punt van het aardoppervlak dezelfde waarde hebben, als de tijdbepaling plaatsvindt volgens de behandelde tijdschaal.
Afhankelijk van de plaats op aarde
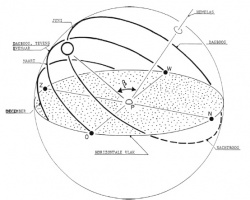
Om punt P wordt ook nu een bol geslagen. Zie figuur 7. De doorsnijding van deze bol met het horizontale vlak wordt horzon genoemd. Het snijpunt van de vertikaal door punt P met de bol heet pool, ook wel zenit. De doorsnijding van de bol met een willekeurig plat vlak door de vertikaal heet verticaalcirkel.
De positie van punt S wordt nu vastgelegd door middel van booglengten langs de horizon en bij S behorende verticaalcirkel. Deze booglengten worden repectievelijk "azimut" en "hoogte" genoemd. Het azimut wordt gemeten vanuit het zuidpunt in oostelijke richting en wordt uitgedrukt in de daarmee corresponderende middelpuntshoek a. De hoogte wordt gemeten vanaf de horizon en eveneens in de daarbij behorende middelpuntshoek h uitgedrukt. De positie van een ster, en daarmee azimut en hoogte, verandert in de tijd. Een uitzondering wordt gevormd door de poolster, omdat deze op de hemelas is gelegen. In Nederland geldt hiervoor dus altijd, dat a = 180° en h = 52°.
Omdat de hoek tussen hemelas en de noord-zuidlijn gelijk is aan de breedtegraad van punt P, kan de volgende conclusie worden getrokken:
Wanneer de plaats van een hemellichaam wordt vastgelegd ten opzichte van het hier beschreven stelsel, dan geldt voor de waarde, die azimut en hoogte op een gegeven tijdstip aannemen, dat deze per breedtegraad verschilt. Depositiebepaling is dus plaatsafhankelijk.
Dagbogen
In de vorige paragraaf is aangetoond, dat elk hemellichaam een schijnbare cirkelbaan beschrijft in een vlak, loodrecht op de hemelas.Dit geldt ook voor de zon. Het zichtbare gedeelte van de zonnebaan wordt dagboog genoemd, het niet zichtbare gedeelte heet nachtboog. In figuur 8. zijn de dagbogen van de zon op de winterdag, lentedag (herfstdag) en zomerdag getekend. De hoek β (zie ook figuur 6) bedraagt op die data repectievelijk 90° + α, 90° en 90° - α. De hoek α is de hoek tussen de hemelas en de ecliptica-as.
Omdat de grootte van β van dag tot dag iets verandert, krijgt waarnemer in punt P de indruk, dat de zon een schroefbeweging uitvoert rond de hemelas.
De schijnbare zonnebaan wordt in 24 uur eenmaal doorlopen. Omdat dit met een constante snelheid gebeurt, is de lengte van een dag evenredig met de lengte van de dagboog. Uit figuur 8 volgt, dat de lengte van een dag in een bepaalde plaats op aarde verandert in de tijd. Op een gegeven datum is de lengte van de dag echter afhankelijk van de geografische breedte van punt P.
Dit is eenvoudig in te zien, door na te gaan doe de in figuur 8. getekende dagboog voor 21 juni verandert als punt P op de evenaar zou zijn gelegen. De hemelas ligt dan in het horizontale vlak en de snijpunten van de schijnbare zonnebaan met het horizontale vlak leveren dag een dagboog, die kleiner is dan de, in figuur 8. voor die datum getekende, dagboog en die precies gelijk is aan een halve cirkelboog.
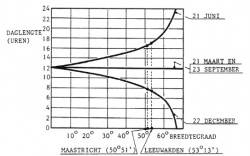
In figuur 9 is voor de drie kenmerkende data in een jaar aangegeven, hoe de lengte van de dag verloopt als functie van de geografische breedte.
Tijdbepaling
Voor onze tijdsbepaling kunnen een aantal tijdschalen worden gehanteerd. Allereerst worden twee tijdschalen bekeken, die gebonden zijn aan de plaats van de waarnemer op aarde.
De tijd, behorende bij de in paragraaf Plaatsbepaling van een ster aan de hemel besproken tijdschaal, wordt zonnetijd genoemd en afgekort tot Z.T. Om 12 uur Z.T. staat de zon altijd op zijn hoogst.
Wanneer met behulp van een uurwerk de tijdsduur wordt gemeten tussen twee achtereenvolgende culminaties van de zon, dan blijkt dat deze niet precies 24 uur te bedragen. Dit verschijnsel wordt veroorzaakt door het variëren van de afstand tussen zon en aarde, het variëren van de omloopssnelheid van de aarde ten opzichte van de zon ('s zomers 29,3 km/s en 's winters 30,3 km/s en door de scheefstand van de aardas. De door onze uurwerken aangegeven tijd wordt middelbare tijd genoemd en afgekort tot M.T. Overeengekomen is, dat op 25 december 12 uur Z.T. samenvalt met 12 uur M.T. Nu blijkt, dat samenvallen van de Z.T.-tijdschaal met de M.T.-schaal ook optreed op 15 april, 14 juni en 1 september.
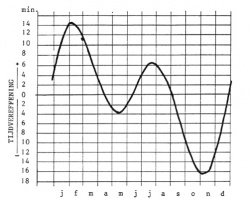
Het aantal minuten, dat bij 12 uur Z.T. mot worden opgeteld om het tijdstip van culminatie van de zon te verkrijgen, gemeten volgens M.T, wordt tijdvereffening genoemd. In figuur 10 is de tijdvereffening uitgezet als functie van de tijd. De zo verkregen kromme wordt tijdsvereffeningskromme genoemd.
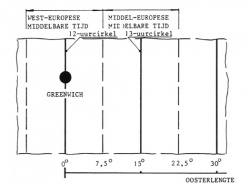
Het aardoppervlak is verdeeld in 24 zones, waarbinnen volgens dezelfde tijdschaal wordt gemeten. Deze zones worden gevormd door lengtecirkels, die 15° uiteen zijn gelegen. Het midden van deze zones wordt gevormd door lengtecirkels, die uurcirkels worden genoemd, Internationaal is overeengekomen dat de 0°-lengtecirkel (Greenwich) de 12-uurcirkel vormt. Zie figuur 11.
De 24-uurscirkel, tevens 0 uurcirkel, vormt de zogenaamde datumgrens. Deze ligt ten oosten van Nieuw-Zeeland. In de zones rond de 12- en 13-uurcirkel wordt gemeten volgens respectievelijk West-Europese M.T. Ondanks het feit dat Nederland geheel binnen de zone is gelegen, waarin moet worden uitgegaan van West-Europese M.T. en Middel-Europese M.T., wordt in ons land met de Middel-Europese M.T. gewerkt.
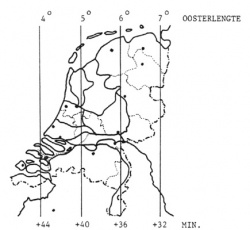
In figuur 12 is aangegeven, hoeveel minuten bij de plaatselijke M.T. moeten worden opgesteld om deze tijd om te zetten in Middel-Europese M.T.