Difference between revisions of "Mechanica"
Frschnater (Talk | contribs) |
Frschnater (Talk | contribs) |
||
| Line 8: | Line 8: | ||
[[File:plaatje6.jpg|780px]] | [[File:plaatje6.jpg|780px]] | ||
| + | Een centrisch geplaatste kracht veroorzaakt een gelijkmatig verdeelde spanning (figuur 1).<br> | ||
| + | Als de kracht een kleine excentriciteit krijgt, komt er buigspanning bij, die een variërende spanning veroorzaakt. (figuur 2). <br> | ||
| + | Als de excentriciteit groter word, komt de situatie dat aan de linkerkant de spanning nul wordt. (figuur 3). Dan is de buigtrekspanning gelijk aan de drukspanning door de normaalkracht.<br> | ||
| + | Bij nog grotere excentriciteit treedt aan de linkerkant trekspanning op. (figuur 4) | ||
| + | |||
| + | In de situatie van figuur 3 is de buigtrekspanning gelijk [[File:formule1.jpg|50px]] aan de spanning [[File:formule1.jpg|50px]] . | ||
| + | Als het moment M gelijk is aan [[File:formule1.jpg|50px]] dan geldt voor de excentriciteit e dat [[File:formule1.jpg|50px]]. | ||
| + | Bij een rechthoekige doorsnede met hoogte h en breedte b geldt:[[File:formule1.jpg|50px]] en [[File:formule1.jpg|50px]]en daaruit volgt dat [[File:formule1.jpg|50px]]. | ||
[[Category:Bachelor 2]] | [[Category:Bachelor 2]] | ||
[[Category: Bachelor 4]] | [[Category: Bachelor 4]] | ||
[[Category: Vakgebieden]] | [[Category: Vakgebieden]] | ||
Revision as of 12:10, 20 February 2012
Nog in de maak...
De kern van een doorsnede.
Als op een doorsnede een normaalkracht werkt zullen in die doorsnede spanningen optreden.
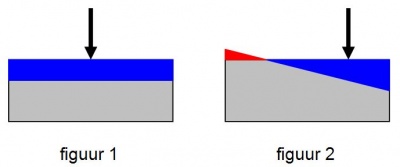
Als de normaalkracht aangrijpt in het zwaartepunt van de doorsnede, zijn de spanningen constant en worden berekend met de formule: ![]() (figuur 1)
(figuur 1)
Als de kracht excentrisch staat, is de spanning niet meer gelijkmatig verdeeld maar verloopt lineair (figuur 2, blauw is druk en rood is trek). Dit wordt veroorzaakt doordat een excentrische kracht kan worden ontbonden in een centrische kracht en een moment. De combinatie van de spanningen door de normaalkracht en een moment resulteert in een lineair verlopend spanningsdiagram, dat kan worden berekend met de formule: ![]() .
.
Als de excentriciteit varieert, verandert de grootte van het moment en daarmee het verloop van de spanningen. Dat kan worden onderzocht met deze animatie , de kracht kan met de muis worden verplaatst. Ook kan worden aangegeven of de doorsnede trekspanningen kan opnemen. Als de doorsnede geen trekspanningen kan opnemen, dan worden de spanningen op een andere manier verdeeld.
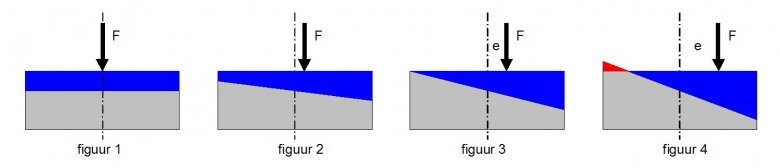
Een centrisch geplaatste kracht veroorzaakt een gelijkmatig verdeelde spanning (figuur 1).
Als de kracht een kleine excentriciteit krijgt, komt er buigspanning bij, die een variërende spanning veroorzaakt. (figuur 2).
Als de excentriciteit groter word, komt de situatie dat aan de linkerkant de spanning nul wordt. (figuur 3). Dan is de buigtrekspanning gelijk aan de drukspanning door de normaalkracht.
Bij nog grotere excentriciteit treedt aan de linkerkant trekspanning op. (figuur 4)
In de situatie van figuur 3 is de buigtrekspanning gelijk ![]() aan de spanning
aan de spanning ![]() .
Als het moment M gelijk is aan
.
Als het moment M gelijk is aan ![]() dan geldt voor de excentriciteit e dat
dan geldt voor de excentriciteit e dat ![]() .
Bij een rechthoekige doorsnede met hoogte h en breedte b geldt:
.
Bij een rechthoekige doorsnede met hoogte h en breedte b geldt:![]() en
en ![]() en daaruit volgt dat
en daaruit volgt dat ![]() .
.