Zonnestralingsrichting
De richting van de zonnestraling is sterk bepalend voor de manier, waarop het verschijnsel bezonning door de mens wordt ervaren. Aan de hand van hetgeen in het artikel Kosmografie wordt besproken, zal hier formules worden afgeleid voor de bepaling van de richting van de zonnestraling als functie van de tijd. Met behulp van deze formules kunnen tabellen, grafieken en diagrammen worden gemaakt, waarvan er een aantal zullen worden behandeld.
Contents
Declinatie en uurhoek
De in de afbeelding over deklinatie en uurhoek getekende hoeken zoals u en d leggen de stralingsrichting vast. Op iedere datum geldt: d = constant. Deze constante kan op de n- de dag van het jaar met grote nauwkeurigheid worden berekend met behulp van formule 1:
D = 23,44° sin {360°(284 + n)/365} (1)
Eveneens op iedere datum geldt, dat:
U = t x 15° (2)
met t gelik aan de tijd in uren volgens Z.T. Met gehulp van (1) en (2) kan nu de stralingsrichting worden gevonden op ieder gewenst tijdstip op iedere gewenste datum.
Azimut en zonshoogte
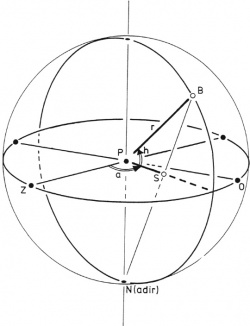
De stralingsrichting is ook vast te leggen met behulp van de hoeken a en h. Zie de figuur over Azimut en zonshoogte. In appendix A is afgeleid, hoe deze hoeken kunnen worden geschreven als functie van de zojuist genoemde hoeken u en d. Het blijkt handiger om h te schrijven als functie van u en d en om a te schrijven als functie van u, d en h.
Gevonden wordt:
h = arcsin (sin ф sin d – cos ф cos d cos u) (3)
a = arcsin { (cos d sin u) / cos h } (4)
De hoek ф is gelijk aan de breedtegraad van de plaats op aarde, waar a en h moeten worden bepaald. De waarden, die a en h aannemen, zijn nu dus plaatsafhankelijk.
Opmerking: voor de berekening van de hoeken a en h bestaan ingewikkelder formules.
Deze beschrijven de hoeken als functie van de middelbare tijd en geven inzicht in het verschijnsel tijdvereffening. Zie (3).
Grafieken, tabellen en diagrammen
Grafieken
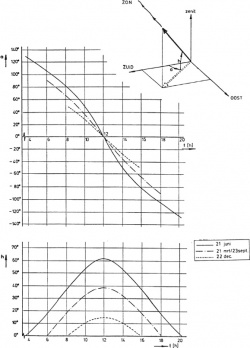
De hoeken u en d en de hoeken a en h kunnen in grafieken worden uitgezet als functie van de tijd. Omdat de hoek d op een bepaalde dag constant is en omdat de hoe u zeer eenvoudig is te berekening, is presentatie van deze hoeken in grafiekvorm nauwelijks zinvol. Dit ligt duidelijk anders voor de hoeken a en h. In figuur 1 is het verloop van deze hoeken als functie van de tijd grafisch weergegeven voor de drie kenmerkende data in het jaar.
Tabellen
Om de zojuist genoemde redenen is tabelleren van de hoeken u en d niet zinvol; alleen de hoeken a en h worden getabelleerd. Zie tabel 1.
| 22 december | 21 maart / 23 september | 21 juni | ||||
| a | h | a | h | a | h | |
| 4.00 | 127° 22' | 1° 47' | ||||
| 5.00 | 116° 00' | 9° 39' | ||||
| 6.00 | 104° 58' | 18° 17' | ||||
| 7.00 | 78° 05' | 9° 10' | 93° 45' | 27° 23' | ||
| 8.00 | 65° 32' | 17° 56' | 81° 40' | 36° 35' | ||
| 9.00 | 40° 37' | 4° 55' | 51° 46' | 25° 48' | 67° 42' | 45° 29' |
| 10.00 | 27° 46' | 10° 06' | 36° 14' | 32° 13' | 50° 17' | 53° 24' |
| 11.00 | 14° 08' | 13° 24' | 18° 47' | 36° 29' | 27° 39' | 59° 14' |
| 12.00 | 0 | 14° 32' | 0 | 38° 00' | 0 | 61° 28' |
| 13.00 | -14° 08' | 13° 24' | -18° 47' | 36° 29' | -27° 39' | 59° 14' |
| 14.00 | -27° 46' | 10° 06' | -36° 14' | 32° 13' | -50° 17' | 53° 24' |
| 15.00 | -40° 37' | 4° 55' | -51° 46' | 25° 48' | -67° 42' | 45° 29' |
| 16.00 | -65° 32' | 17° 56' | -81° 40' | 36° 35' | ||
| 17.00 | -78° 05' | 9° 10' | -93° 45' | 27° 23' | ||
| 18.00 | -104° 58' | 18° 17' | ||||
| 19.00 | -116° 00' | 9° 39' | ||||
| 20.00 | -127° 22' | 1° 47' | ||||
| Zon op zon onder |
08.15 15.45 |
06.00 18.00 |
03.45 20.15 | |||
Tabel 1: Azimut en zonshoogte op de drie kenmerkende data voor 52° N.B. - uit apart bestand
Diagrammen
Allereerst wordt gekeken naar de tot standkoming en gebruik van een veel toepast diagram, waaruit azimut en zonshoogte op een bepaalde datum rechtstreeks kunnen worden afgelezen als functie van tijd.
Om punt P, gelegen in het horizontale vlak, wordt een bol geslagen met straar r. Zie figuur 2. De lijn vanuit P in de richting van de zon snijdt deze bol in punt B. Punt S is het snijpunt van het lijnstuk BN met het horizontale vlak. De hoek tussen het lijnstuk PS en de zuidrichting is nu gelijk aan azimut. De lengte 1 van het lijnstuk PS is een maat voor zonshoogte.
In appendix B is afgeleid, dat voor deze lengte geldt:
1 = r tg \{ (90° - h)/2\} (5)
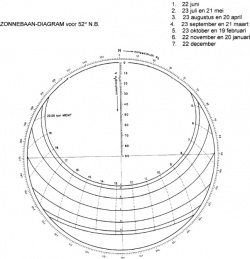
De hoeken a en h zijn bekend als functie van de tijd en daarmee dus ook grootte en richting van het lijnstuk PS. Wanneer nu voor een bepaalde datum grootte en richting van het lijnstuk PS worden uitgezet als functie van de tijd vanuit punt P, ontstaat de baan, die door punt S wordt beschreven in het horizontale vlak. Het diagram, dat bijv. voor 56° N.B. op deze wijze ontstaat, is te zien in figuur 3.
Rond punt P zijn cirkels getrokken. De straal hiervan is gelijk aan de waarde van 1, behorend bij zonshoogten gelijk aan h = 0°, 10°, 20°, … 90°. De waarde van h is bij de daarmee corresponderende cirkel vermeld. Duidelijk is, dat voor elke breedtegraad een afzonderlijk diagram moet worden geconstrueerd.
Behandeld wordt nu een diagram, waaruit het azimut direct, en de zonshoogte indirect is af te lezen als functie van de tijd.
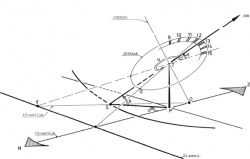
In punt P van het horizontale vlak wordt het verticale lijnstuk PT opgericht met lengte H. Zie figuur 4. De lijn door punt T, in de richting van de zon, snijdt het horizontale vlak in punt S. Het lijnstuk PS is de projectie van het lijnstuk PT op het horizontale vlak tengevolge van de zonnestraling. De baan, die door punt S gedurende een dag wordt doorlopen, is te bepalen als grootte en richting van het lijnstuk PS bekend zijn. De grootte van dit lijnstuk wordt aangegeven met 1 en wordt met behulp van de betrekking:
1 = H cotg h (6)
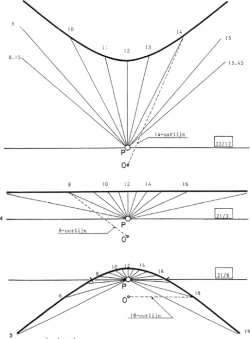
De richting van het lijnstuk PS wordt vastgelegd met behulp van de hoek tussen dit lijnstuk en de lijn vanuit punt P in noordelijke richting. Deze hoek is gelijk aan het azimut. De baan, die door punt S op 22 december, 21 maart (23 september) en 21 juni wordt beschreven op bijvoorbeeld 52° N.B. kan nu worden geconstrueerd. Wanneer dit wordt gedaan voor een waarde van H = 0.015m, dan ontstaan de in figuur 5. afgebeelde "schaduwdiagrammen". Hierin zijn ook grootte en richting van het lijnstuk PS aangegeven op de hele uren.
De richting van het lijnstuk PS op een willekeurig tijdstip kan nu worden geschat en de daarbij behorende grootte van het lijnstuk worden opgemeten. De zonshoogte kan dan worden berekend met behulp van de betrekking
H = arctg (H/1) (7)
Wanner voor alle data het punt S zou worden bepaald op een gegeven tijdstip, bijvoorbeeld 15.00 uur, dan zou blijken dat punt S altijd op een rechte lijn is gelegen die de noord-zuidlijn snijdt in punt 0. Dit is aan te tonen door de hemelas door punt T en het platte vlak, loodrecht op de hemelas en eveneens door punt T, te tekenen. Zie figuur 4.
De uurhoek u heeft op een gegeven tijdstip op alle data dezelfde waarde en de lijn door de punten T en V, die in het platte vlak door T, loodrecht op de hemelas is gelegen, heeft dus op dat tijdstip altijd dezelfde richting. Alleen de declinatie verschilt van dag tot dag. Eenvoudig is nu aan te tonen, dat op iedere datum om 15.00 uur geldt, dat het lijnstuk TS is gelegen in het vlak door punten 0, T en V. Hiermee is dan aangetoond, dat punt S altijd om 15.00 uur op de lijn door de punten 0 en V ligt.
De lijn door het punt 0 en het punt V op de tijdstippen t = 0, 1, 2, ………24 uur wordt respectievelijk, 0-uurlijn, 1-uurlijn, 2-uurlijn………24-uurlijn….24-uurlijn genoemd. In figuur 4. zijn de 12-uurlijn en de 15-uurlijn getekend. Zie ook figuur 5.
Uit de hierboven besproken formules en diagrammen kunnen een aantal belangrijke conclusies worden getrokken:
- Op de tijdstippen t1 en t2 = 24 – t1 (t1 in uren volgens Z.T.) geldt voor azimu en zonshoogte respectievelijk:
a (t2) = 360° - a (t1) h (t2) = h (t1)
- Voor t = 12.00 uur (Z.T.) geldt altijd:
a = 0° h = h maximum
- Alleen op 21/3 (en dus op 23/9) gaat de zon precies in het oosten op en precies in het Westen onder.T
- Tussen de keerkringen ( op 23,46° N.B. en 23, 46° Z.B.) en de polen geldt, dat de zonshoogte 's winters het kleinst en 's zomers het grootst is.
- Elk van de besproken diagrammen is slechts geldig voor een bepaalde breedtegraad.